variila soldadura y algo para cortar en este caso un arco
Blog POLIEDROS
Sígueme para aprender cómo ser un Blogger
Mi Blog
17Aug
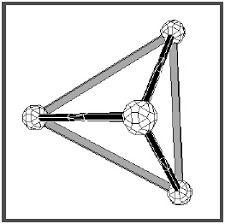
Como ya se ha mencionado, el número total de poliedros de caras regulares es infinito, y se puede comprobar fácilmente mediante el siguiente ejercicio mental: Supongamos que tenemos en nuestras manos 2 tetraedros iguales construidos en cartón. Podemos comproboar que ambos son poliedros de caras regulares ya que cada uno está compuesto por 4 triángulos equiláteros. Entonces, los unimos con pegamento por sus bases. El cuerpo que obtendríamos (una bipirámide triangular) seguiría siendo un poliedro regular ya que todas sus caras siguen siendo polígonos regulares. Ahora, tomamos un tercer tetraedro, igual a los 2 anteriores, y lo unimos por su base con cualquiera de la caras de la bipirámide. Se puede comprobar que el poliedro que obtenido aún sigue teniendo caras regulares
17Aug
Los 5 poliedros regulares o Sólidos Platónicos, que cumplen la condición de que todas sus caras y ángulos son iguales: El tetraedro. El cubo o hexaedro regular. El octaedro. El dodecaedro. El icosaedro.
17Aug
son caras, vértices y aristas. Las caras son los polígonos que la limitan. Las aristas son los lados de las caras, y limitan dos caras contiguas. Los vértices son los de las caras. En cada vértice de un poliedro concurren tres o más caras.
17Aug
Los poliedros son elementos geométricos que disponen de caras planas y que albergan un volumen que no es infinito. Las raíces etimológicas del término, que se hallan en la lengua griega, refieren a “muchas caras”.
Un poliedro puede ser entendido como un cuerposólido y tridimensional. Cuando todas sus caras y ángulos son iguales entre sí, se lo califica como un poliedro regular. De lo contrario, será un poliedro irregular.
Otra clasificación posible está vinculada a la cantidad de caras que presenta. Un poliedro de seis caras recibe el nombre de hexaedro, un poliedro de cinco caras se conoce como pentaedro y así sucesivamente, formando siempre la denominación con el prefijo griego correspondiente (hexa, penta, tetra, etc.).
Por otra parte, se puede diferenciar entre poliedros cóncavos y poliedros convexos. Los poliedros cóncavos son aquellos que, al unir dos puntos situados dentro del cuerpo, el segmentocorrespondiente sale de la superficie. En cambio, en los poliedros convexos, los segmentos que vinculan dos puntos del espacio interior nunca salen del cuerpo geométrico.
ACERCA
HAREMOS UN JARDÍN DE POLIEDROS DE LA INGENIERÍA MECÁNICA
ALUMNOS DEL PRIMER SEMESTRE CON AYUDA DE ALUMNOS DE QUINTO SEMESTRE
ALUMNOS DEL PRIMER SEMESTRE CON AYUDA DE ALUMNOS DE QUINTO SEMESTRE
francois viete
Información de Francois Viete
My name is Francois Viete
i was born is Paris, France
Mi nationaly ench, mi year, of birth in 1540
There is no information about my family i am famous for my work in root extraction and was for my bublication of books.
my alma mater university of Poitiers.
I was the first to present the parameters of an equation by letter, being an outs tonding precursor of the use of the use of Algebra in Criptographi.
I died in 13 december 1603
My name is Francois Viete
i was born is Paris, France
Mi nationaly ench, mi year, of birth in 1540
There is no information about my family i am famous for my work in root extraction and was for my bublication of books.
my alma mater university of Poitiers.
I was the first to present the parameters of an equation by letter, being an outs tonding precursor of the use of the use of Algebra in Criptographi.
I died in 13 december 1603
